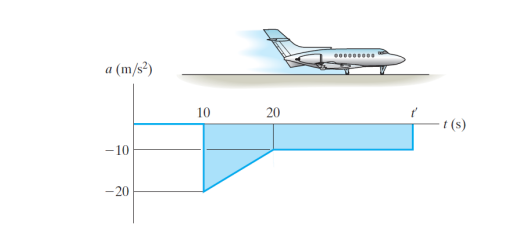
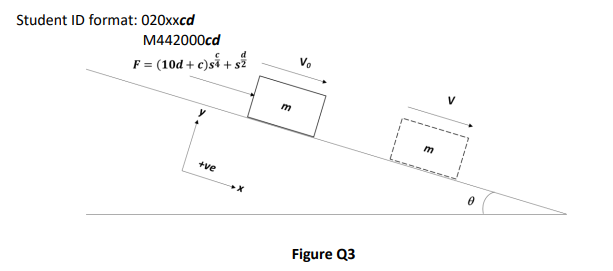
Figure Q3
Given that a block with mass, m, slides on an inclined ramp (θ with horizontal) shown in Figure Q3 with an applied force of F. The coefficient of kinetic friction between the ramp and block is μk. The initial velocity is V0 and the final velocity is V. Determine the sliding distance, s.
The parameters mentioned above takes the form of:
m = 20 − c/2
θ = 30 − c − 0.1d
F = (10d + c)sc/4 + sd/2
μk = 0.4 − d/100
V = 1.1c + d + 0.2
V0 = c + 0.1d + 0.05
Application of Newton-Raphson Method in Dynamics Using the Work-Energy Principle
In Dynamics, the work-energy principle relates the work done by all forces on a particle to its change in kinetic energy. It is expressed as:
T1 + Vg,1 + Ve,1 + ∑U1→2 = T2 + Vg,2 + Ve,2
where:
T1 and T2 are the initial and final kinetic energies, respectively;
Vg,1 and Vg,2 are the initial and final gravitational potential energies, respectively;
Ve,1 and Ve,2 are the initial and final elastic energies, respectively; and
U1→2 is the work done by all forces (applied force, frictional force etc) as the particle moves from position 1 to position 2.
In many practical problems, especially involving friction or nonlinear forces, the sliding distance is not directly solvable through algebraic manipulation because it appears within a nonlinear equation derived from the work-energy expression. For such cases, numerical methods like the Newton-Raphson method are essential.
Get 30% Discount on This Assignment Answer Today!
Why Newton-Raphson?
The Newton-Raphson method is an efficient iterative root-finding technique for solving nonlinear equations of the form f(s) = 0. When the equation resulting from the work-energy principle is nonlinear in terms of the distance s, we can rewrite it as:
f(s) = T1 + Vg,1 + Ve,1 + ∑U1→2 − T2 − Vg,2 − Ve,2 = 0
We then apply the Newton-Raphson iterative formula:
sn+1 = sn − f(sn)/f'(sn)