Convincing Features

School
*We aren't endorsed by this school
Assignment Type
Subject
Uploaded by Malaysia Assignment Help
Date
Problem Statement
The determination of the fundamental natural frequency for cantilever beams is crucial in many engineering applications. Here, a cantilever beam refers to a beam that is fixed on one end and free on the other end as shown in Figure 1 below.
Generally, a cantilever beam would have an infinite number of natural frequencies corresponding to its vibration modes. However, the fundamental natural frequency refers to the natural frequency of the beam under its first vibration mode. For thin beams, the Euler-Bernoulli beam theory can be used to determine this natural frequency.
The fundamental natural frequency of a cantilever beam is determined by the following equation:
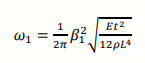
where 𝜔1 is the fundamental natural frequency of the beam in Hz, 𝐸 is the beam Young’s modulus, 𝑡 is the thickness of the beam, 𝜌 is the beam’s density, 𝐿 is the length of the beam and 𝛽1 is the fundamental eigenfrequency of the beam which can be determined as the smallest absolute value from the characteristic equation of the following matrix in equation (2). In equation (2), 𝑛 corresponds to the vibration mode number.
